440 lines
13 KiB
Text
440 lines
13 KiB
Text
{
|
|
"cells": [
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "f37ff61d-dfe1-4b65-a74d-efe317bbfade",
|
|
"metadata": {},
|
|
"source": [
|
|
"# Data Structures: Trees, Graphs, and Tries"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "c12455f1-b6e7-4822-8b20-0da02e8e7a11",
|
|
"metadata": {},
|
|
"source": [
|
|
"We saw that linked lists use nodes linked in a linear fashion.\n",
|
|
"\n",
|
|
"Each node had a \"next\" (and possibly a reference to \"prev\").\n",
|
|
"\n",
|
|
"We can use this same idea with additional links to create **Trees**.\n",
|
|
"\n",
|
|
"We'll start with a classic **binary search tree**.\n",
|
|
"\n",
|
|
"Each node has a value, and up to two children, \"left\" and \"right\".\n",
|
|
"\n",
|
|
"Data is stored in the tree such that when a new node is added, if it is less than the current value of a node, it should be stored to the left, and if it is greater, it should be stored to the right.\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 5,
|
|
"id": "012f2a24-f0cc-47ef-a572-3c0825f27850",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"source": [
|
|
"class Node:\n",
|
|
" def __init__(self, value, left=None, right=None):\n",
|
|
" self.value = value\n",
|
|
" self.left = left\n",
|
|
" self.right = right\n",
|
|
"\n",
|
|
" def __str__(self):\n",
|
|
" return f\"({self.value}, {self.left}, {self.right})\"\n",
|
|
"\n",
|
|
"\n",
|
|
"class BST:\n",
|
|
" def __init__(self, iterable=None):\n",
|
|
" self.root = None\n",
|
|
" if iterable:\n",
|
|
" for item in iterable:\n",
|
|
" self.add_item(item)\n",
|
|
"\n",
|
|
" def add_item(self, newval):\n",
|
|
" # special case: first item\n",
|
|
" if self.root is None:\n",
|
|
" self.root = Node(newval)\n",
|
|
" else:\n",
|
|
" parent = self.root\n",
|
|
" # traverse until we find room in the tree\n",
|
|
" while True:\n",
|
|
" if newval < parent.value:\n",
|
|
" if parent.left:\n",
|
|
" parent = parent.left\n",
|
|
" else:\n",
|
|
" parent.left = Node(newval)\n",
|
|
" break\n",
|
|
" else:\n",
|
|
" if parent.right:\n",
|
|
" parent = parent.right\n",
|
|
" else:\n",
|
|
" parent.right = Node(newval)\n",
|
|
" break\n",
|
|
"\n",
|
|
"\n",
|
|
"def print_infix(node):\n",
|
|
" \"\"\"prints items in sorted order\"\"\"\n",
|
|
" if node.left:\n",
|
|
" print_infix(node.left)\n",
|
|
" print(node.value)\n",
|
|
" if node.right:\n",
|
|
" print_infix(node.right)\n",
|
|
" "
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "c833bb06-4b02-4f50-bab9-ab1d30092144",
|
|
"metadata": {},
|
|
"source": [
|
|
"Tree traversal is inherently recursive, so we'll use a recursive function to print the tree in sorted order.\n",
|
|
"\n",
|
|
"Most tree algorithms will operate on the left & right subtrees the same way, so we can write a recursive function that takes a node and calls itself on the left & right subtrees."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 7,
|
|
"id": "4f652851-2fbd-42c1-adb3-cb352657bb5a",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"name": "stdout",
|
|
"output_type": "stream",
|
|
"text": [
|
|
"Bear\n",
|
|
"Fox\n",
|
|
"Rabbit\n",
|
|
"Raccoon\n",
|
|
"Wolf\n"
|
|
]
|
|
}
|
|
],
|
|
"source": [
|
|
"tree = BST()\n",
|
|
"tree.add_item(\"Fox\")\n",
|
|
"tree.add_item(\"Wolf\")\n",
|
|
"tree.add_item(\"Bear\")\n",
|
|
"tree.add_item(\"Raccoon\")\n",
|
|
"tree.add_item(\"Rabbit\")\n",
|
|
"print_infix(tree.root)\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "44e92462-532b-4340-8c9b-52314870677f",
|
|
"metadata": {},
|
|
"source": [
|
|
"#### Aside: defaultdict\n",
|
|
"\n",
|
|
"```python\n",
|
|
"# common pattern:\n",
|
|
"if key not in dct:\n",
|
|
" dct[key] = []\n",
|
|
"dct[key].append(element)\n",
|
|
"```\n",
|
|
"\n",
|
|
"We can instead use `collections.defaultdict`:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 6,
|
|
"id": "a06805c2-75ae-46e3-9916-f4ee8cca6080",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"name": "stdout",
|
|
"output_type": "stream",
|
|
"text": [
|
|
"{1, 2, 3}\n",
|
|
"defaultdict(<function <lambda> at 0x111069120>, {'newkey': {1, 2, 3}})\n",
|
|
"defaultdict(<function <lambda> at 0x111069120>, {'newkey': {1, 2, 3, 4}})\n"
|
|
]
|
|
}
|
|
],
|
|
"source": [
|
|
"from collections import defaultdict\n",
|
|
"\n",
|
|
"# give defaultdict a function that it will use to generate missing keys\n",
|
|
"dd = defaultdict(lambda: {1, 2, 3})\n",
|
|
"\n",
|
|
"print(dd[\"newkey\"])\n",
|
|
"print(dd)\n",
|
|
"\n",
|
|
"dd[\"newkey\"].add(4) # can add to set without ensuring it exists\n",
|
|
"print(dd)"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "ba2d9950-e5cf-4d11-9307-f1fa37f01e67",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Graphs\n",
|
|
"\n",
|
|
"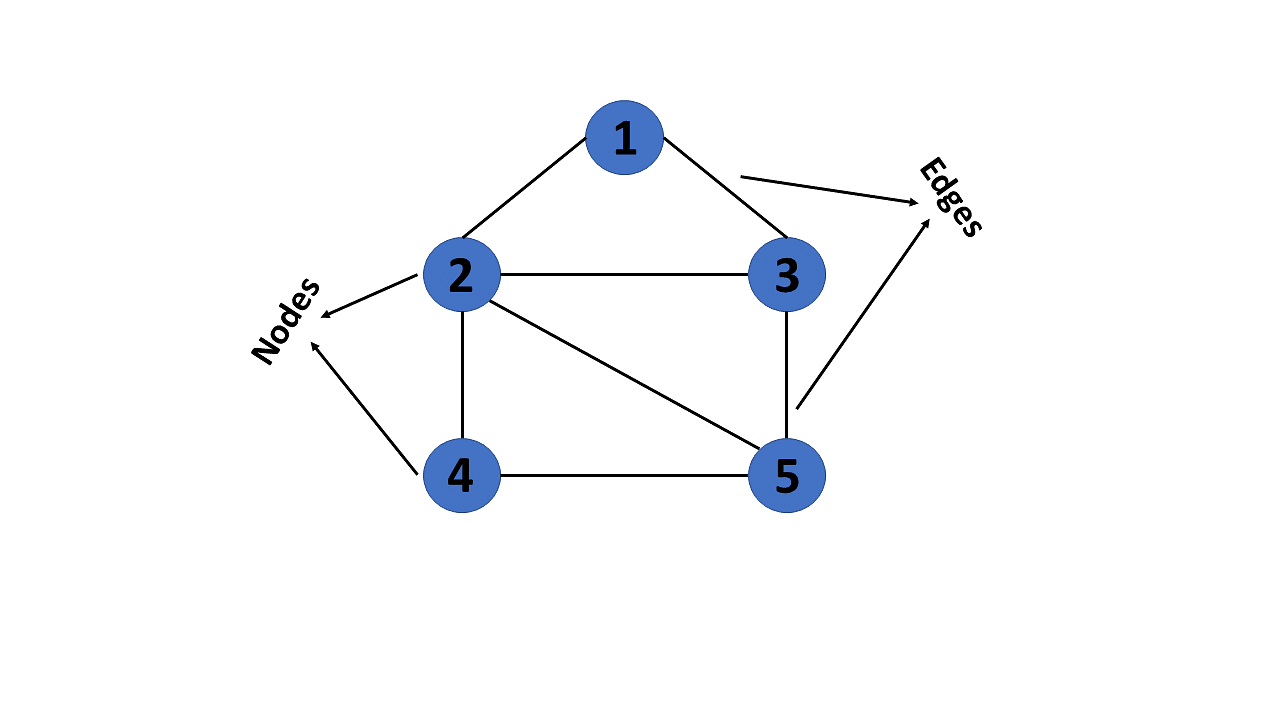"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 13,
|
|
"id": "323a6e33-76b7-41b7-97b9-e4dfa04d6bb4",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"source": [
|
|
"class Graph:\n",
|
|
" def __init__(self):\n",
|
|
" # create a dictionary where every string maps to a set of strings\n",
|
|
" self.edges = defaultdict(set)\n",
|
|
"\n",
|
|
" def add_edge(self, node1, node2):\n",
|
|
" # add in both directions, could alter for directed graph\n",
|
|
" self.edges[node1].add(node2)\n",
|
|
" self.edges[node2].add(node1)\n",
|
|
"\n",
|
|
" def find_path(self, from_node, to_node, seen=None):\n",
|
|
" if not seen:\n",
|
|
" seen = set()\n",
|
|
"\n",
|
|
" if to_node in self.edges[from_node]:\n",
|
|
" return (from_node, to_node)\n",
|
|
" else:\n",
|
|
" for sibling in self.edges[from_node] - seen:\n",
|
|
" return (from_node,) + self.find_path(\n",
|
|
" sibling, to_node, seen | set(sibling)\n",
|
|
" )\n",
|
|
" # return self.find_path("
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 14,
|
|
"id": "867f5186-e308-4d2f-9766-713ecb352f99",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"data": {
|
|
"text/plain": [
|
|
"('A', 'D', 'B')"
|
|
]
|
|
},
|
|
"execution_count": 14,
|
|
"metadata": {},
|
|
"output_type": "execute_result"
|
|
}
|
|
],
|
|
"source": [
|
|
"g = Graph()\n",
|
|
"g.add_edge(\"A\", \"D\")\n",
|
|
"g.add_edge(\"B\", \"D\")\n",
|
|
"g.find_path(\"A\", \"B\")"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 17,
|
|
"id": "a9acaa28-8a24-41c5-86c0-4342365533f6",
|
|
"metadata": {},
|
|
"outputs": [
|
|
{
|
|
"data": {
|
|
"text/plain": [
|
|
"('A', 'B', 'A', 'D', 'E')"
|
|
]
|
|
},
|
|
"execution_count": 17,
|
|
"metadata": {},
|
|
"output_type": "execute_result"
|
|
}
|
|
],
|
|
"source": [
|
|
"g = Graph()\n",
|
|
"g.add_edge(\"A\", \"B\")\n",
|
|
"g.add_edge(\"B\", \"C\")\n",
|
|
"g.add_edge(\"C\", \"D\")\n",
|
|
"g.add_edge(\"D\", \"E\")\n",
|
|
"g.add_edge(\"A\", \"D\")\n",
|
|
"g.find_path(\"A\", \"E\")"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "615230a9-5f7c-47c9-9d5e-83d37081bc47",
|
|
"metadata": {},
|
|
"source": [
|
|
"### Discussion\n",
|
|
"\n",
|
|
"* Graphs & Trees in the real world?\n",
|
|
"* Alternate implementations?\n",
|
|
" * NetworkX"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "45d51cd1-9d2b-40dd-95b2-f51f11b49b9e",
|
|
"metadata": {},
|
|
"source": [
|
|
"## Tries\n",
|
|
"\n",
|
|
"Usually pronounced \"try\" to differentiate it from trees.\n",
|
|
"\n",
|
|
"A **trie** is a data structure that stores data associated with string keys similar to a dictionary in many ways. (Python `dict`s are a different data structure: **hash tables**.)\n",
|
|
"\n",
|
|
"A **trie** is a specialized data structure, particularly useful for partial matching of strings. The way the data is stored enables efficient lookup of all strings that start with a given prefix, as well as \"fuzzy search\" where some characters don't match.\n",
|
|
"\n",
|
|
"Each node in a **trie** contains:\n",
|
|
"\n",
|
|
"- an fixed-size array of children\n",
|
|
"- a value\n",
|
|
"\n",
|
|
"Let's imagine a simplified version of a **trie** that can only store string keys with the letters \"a\", \"b\", \"c\", and \"d\".\n",
|
|
"\n",
|
|
"So keys \"a\", \"ba\", \"dddddd\", and \"abcdabcdaabcad\" would all be valid.\n",
|
|
"\n",
|
|
"Now, instead of `linked_list.next` or `tree_node.left`, we will have four children, so we'll store them in a tuple:"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": 18,
|
|
"id": "1ed75b91-54fe-4650-965d-ef26507788b9",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"source": [
|
|
"\n",
|
|
"class TrieNode:\n",
|
|
" def __init__(self, value=None):\n",
|
|
" self.value = value\n",
|
|
" self.children = [None, None, None, None]\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "4ad2dec4-dc42-48bd-a144-d5c61d60dfdb",
|
|
"metadata": {},
|
|
"source": [
|
|
"Notice that we **do not store the key**!\n",
|
|
"\n",
|
|
"```python\n",
|
|
"trie = Trie()\n",
|
|
"trie[\"a\"] = 1\n",
|
|
"```\n",
|
|
"\n",
|
|
"Represents a tree with a single key \"a\". The node \"X\" is the 0th child of the root node. It would have no children set, and a value of `1`.\n",
|
|
"\n",
|
|
"```\n",
|
|
" root\n",
|
|
" / \\\\\\\n",
|
|
" X\n",
|
|
"//\\\\\n",
|
|
"```\n",
|
|
"Let's look at a trie where someone has also set `trie[\"aba\"] = 100`\n",
|
|
"\n",
|
|
"\n",
|
|
"```\n",
|
|
" root\n",
|
|
" / \\\\\\\n",
|
|
" X \n",
|
|
" /|\\\\\n",
|
|
" Y\n",
|
|
" /\\\\\\\n",
|
|
" Z \n",
|
|
" //\\\\\n",
|
|
"```\n",
|
|
"\n",
|
|
"Each node has four children, the 0th child being associated with the value \"a\", the 1st with \"b\", and so on.\n",
|
|
"\n",
|
|
"- X is the same as before `value=1`. It now has a child node \"Y\" in 1st position, associated with \"b\". \n",
|
|
"- Y has no `value` set, because it only exists to build out the tree in this case. It has a child at \"a\" position (0).\n",
|
|
"- Z is at a terminal position and would have `value=100`. Since the path from the root is \"aba\" that is the key associated with the value."
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "3c397fb5-0503-4d8e-a13d-58b6d5cd6943",
|
|
"metadata": {},
|
|
"source": [
|
|
"### Lookup Algorithm\n",
|
|
"\n",
|
|
"Traversing the tree is done by a simple recursive algorithm:\n",
|
|
"\n",
|
|
"- if there are more letters in the key: convert the next one to an index and traverse to that child node\n",
|
|
"- if there are no more letters: the current node is the destination\n",
|
|
"\n",
|
|
"The correct behavior when encountering a child node that does not (yet) exist depends on the nature of the traversal:\n",
|
|
"\n",
|
|
"In a lookup (such as `__getitem__`) the key in question must not be in the **trie**.\n",
|
|
"If a value was being set, the node should be created.\n",
|
|
"\n",
|
|
"### Note/Project Hint\n",
|
|
"\n",
|
|
"`value=None` will create problems in practice, because you should be able to set `trie[\"abc\"] = None` and not have it treat it as if the data was deleted.\n",
|
|
"\n",
|
|
"Instead, you will probably want to use different values for unset variables. It is common to make a \"sentinel\" class for this, a class that is used to create a unique value (like `None` being the sole instance of `NoneType`.).\n",
|
|
"\n",
|
|
"```python\n",
|
|
"class DefaultColor:\n",
|
|
" \"\"\" Used as a sentinel class. \"\"\"\n",
|
|
"\n",
|
|
"def set_background(color=DefaultColor):\n",
|
|
" \"\"\"\n",
|
|
" This function exists to set the background color.\n",
|
|
" (In reality, to demonstrate a time when you might treat None and an unset value differently.)\n",
|
|
" \n",
|
|
" If color is set to None, the background will be transparent.\n",
|
|
" If color is not set, the background will default to the user's choice.\n",
|
|
" \"\"\"\n",
|
|
" if color is DefaultColor:\n",
|
|
" ...\n",
|
|
"```\n"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "markdown",
|
|
"id": "4aef9799-2f13-4c7c-ae62-ac8e6ed22ca3",
|
|
"metadata": {},
|
|
"source": [
|
|
"### Trie Complexity\n",
|
|
"\n",
|
|
"Trie traversal complexity is `O(m)` where **m** is the length of the key strings. \n",
|
|
"\n",
|
|
"This in practice would likely be much lower than **n**, the number of words in the data.\n",
|
|
"\n",
|
|
"### Discussion\n",
|
|
"\n",
|
|
"- How would prefix lookup work?\n",
|
|
"- Wildcards?"
|
|
]
|
|
},
|
|
{
|
|
"cell_type": "code",
|
|
"execution_count": null,
|
|
"id": "0939902d-b50b-4073-92ab-4df03bc1b6fb",
|
|
"metadata": {},
|
|
"outputs": [],
|
|
"source": []
|
|
}
|
|
],
|
|
"metadata": {
|
|
"kernelspec": {
|
|
"display_name": "Python 3 (ipykernel)",
|
|
"language": "python",
|
|
"name": "python3"
|
|
},
|
|
"language_info": {
|
|
"codemirror_mode": {
|
|
"name": "ipython",
|
|
"version": 3
|
|
},
|
|
"file_extension": ".py",
|
|
"mimetype": "text/x-python",
|
|
"name": "python",
|
|
"nbconvert_exporter": "python",
|
|
"pygments_lexer": "ipython3",
|
|
"version": "3.10.15"
|
|
}
|
|
},
|
|
"nbformat": 4,
|
|
"nbformat_minor": 5
|
|
}
|