---
theme: custom-theme
---
# Perception & Color
## CAPP 30239
---
## Today
- What matters most when creating a visualization?
- How does human **perception** factor into visualization design?
- Understanding **color**, and computational representations of it.
---
## What is the most important question when creating a visualization?
---
## What is the most important question when creating a visualization?
Where will the data come from?
What type of chart do I use?- Who is the audience?
---
## Audience First
- Who are you presenting to?
- How familiar are they with the data?
- What is their numerical & visualization literacy?
- Via what medium will they receive the information?
- What are you trying to do? (Persuade, Inform, Inspire?)
*Only now can we start thinking about data and presentation.*
---
## Perception
- **Selective** - We can only pay attention to so much.
- **Patterns** - Our brains are pattern-matching machines, audience will benefit from intentional patterns & be distracted by unintentional ones.
- **Limited working memory** - We hold a very limited set of information in our minds at once.
---
## What do you see?
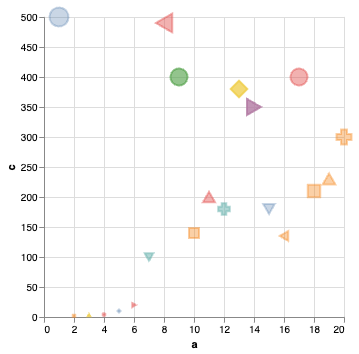
```python
alt.Chart(random_df).mark_point().encode(
alt.X("a"),
alt.Y("c"),
alt.Color("b"),
alt.Size("c"),
alt.Shape("a:N"),
alt.Fill("b"),
alt.Opacity("b"),
)
```
---
## What do you see?
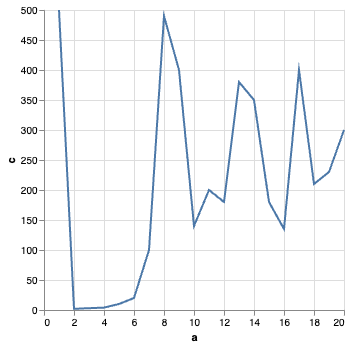
```
alt.Chart(random_df).mark_line().encode(
x="a",
y="c",
)`
```
---
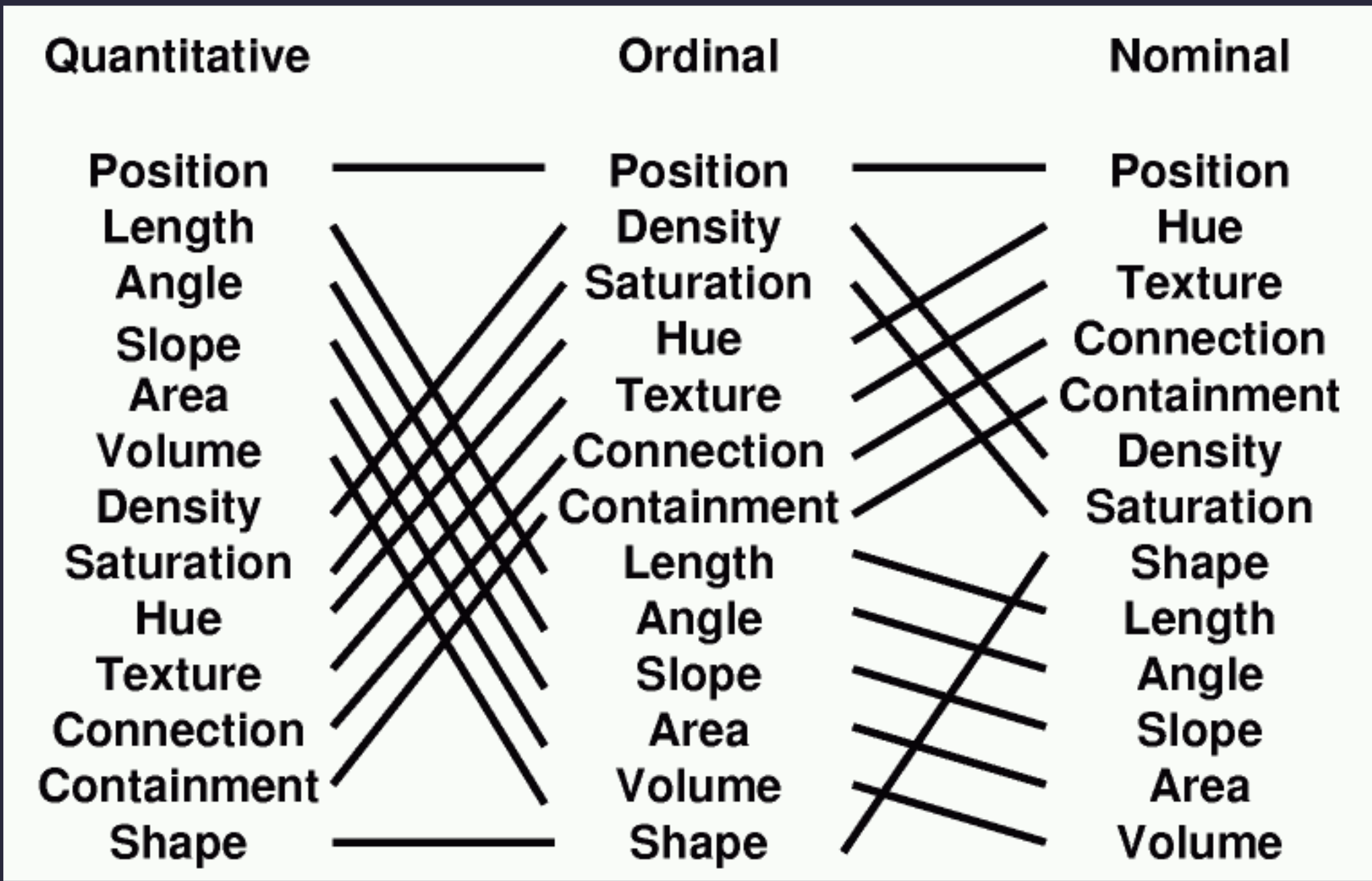
## Effectiveness Revisited
---
**Altair Channels**
- Position (`X, Y`)
- Angle (`Angle`)
- Area (`Radius`, `Size`)
- Hue, Saturation (`Color`)
- Texture (`Opacity`, `Fill`)
- Shape (mark type, `Shape`)
**What about?**
- Length
- Slope
- Volume
- Density
- Connection
- Containment
---
**Derived Properties**�
�
- Length/Area - size of bars (`X`, `Y`)
- Slope & Density - affected by scale
- Connection - ex. layering of lines w/ points
- Containment - achieved with layering
What about *volume*?
---
## Stevens' Power Law
Stevens (1975): Human response to sensory stimulus is characterized by a power law with different exponents with different stimuli.
perception = (magnitude of sensation)a
Smaller a exponent: harder to perceive changes.
Stevens measured values of a by exposing people to varied stimulus and asking them to compare magnitudes.
---
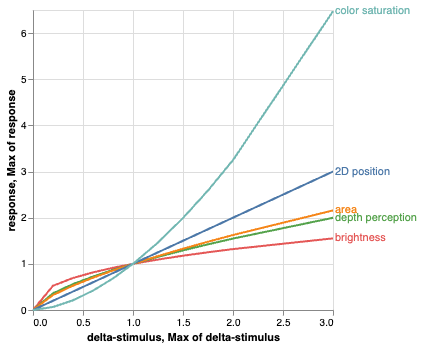
| Continuum | Exponent |
|-|-|
| Color Brightness| 0.33-0.5 |
| Smell| 0.6 |
| Loudness | 0.67 |
| **Depth Perception** | 0.67 |
| Area | 0.7 |
| 2D Planar Position | 1.0 |
| Warmth | 1.3-1.6 |
| Color Saturation | 1.7 |
| Electric Shock | 3.5 |